Motivation

How do you design tools that can protect you against too much user traffic? How does your web application handle slowdowns in downstream services? How do you ask your clients to kindly back off and retry later? How do you guarantee capacity for your most important units of work? Most importantly, how do you know when it's time to take action?

Through my work at Shopify, I have spent many hours of research, prototyping, and building tools to answer those questions and everything related to them. This note will not be anything glamorous editorially speaking (at least to begin with) but I hope to keep updating it over time so I end up with

1. A survey on the state of the industry (see Appendix if this is all you need from me), and
2. Document the thoughts I've repeated for myself and others over time.

If this topic interests you and you'd like to chat, feel free to shoot me an email.

Chapter 1: Load Shedding in Electrical Systems

Surprise! This is a cross-discipline concept! This was the first thing I learnt in 2018. My introduction to this interesting field of research started following an incident in 2018, where too much traffic caused a regional capacity starvation at Shopify.

Load shedding in electrical power delivery gives us much inspiration to go off of:

• Power plants prioritize emergency usage over others: hospitals, police stations, fire stations, etc must be honoured over residential power delivery.
• Handling of sustained overload and momentary overload shall be differentiated.
• A feedback system shall observe the health of your plant, and therefore regulate the load imposed on your circuit.

After learning about load shedding in the electrical engineering discipline, I quickly tried to simulate this phenomena in software. My first prototype was born in 2018.

This was the first diagram I drew:

Chapter 2: The Health Signal

So the first step in creating a capacity control system is to identify whether your plant/platform/application is overloaded or not.

Naively, this could be done in a boolean manner (am I overloaded currently?), however Brendan Gregg offers us the USE method which we can adapt to our systems.

Based on my research, here are a few metrics to think about:

• How many CPUs do you have? How many of your processes are waiting for a CPU? What is your runqueue latency?
• What's the length of the queues in your system?
• What is the average queueing penalty (in time units) that your workload is incurring

In the end, our goal is to monitor our system reliably so that we can react to it appropriately.

Here is a practical example: if you have a finite number of worker processes, and each web request ties up a whole worker process, then your worker utilization is as simple grade-school math:

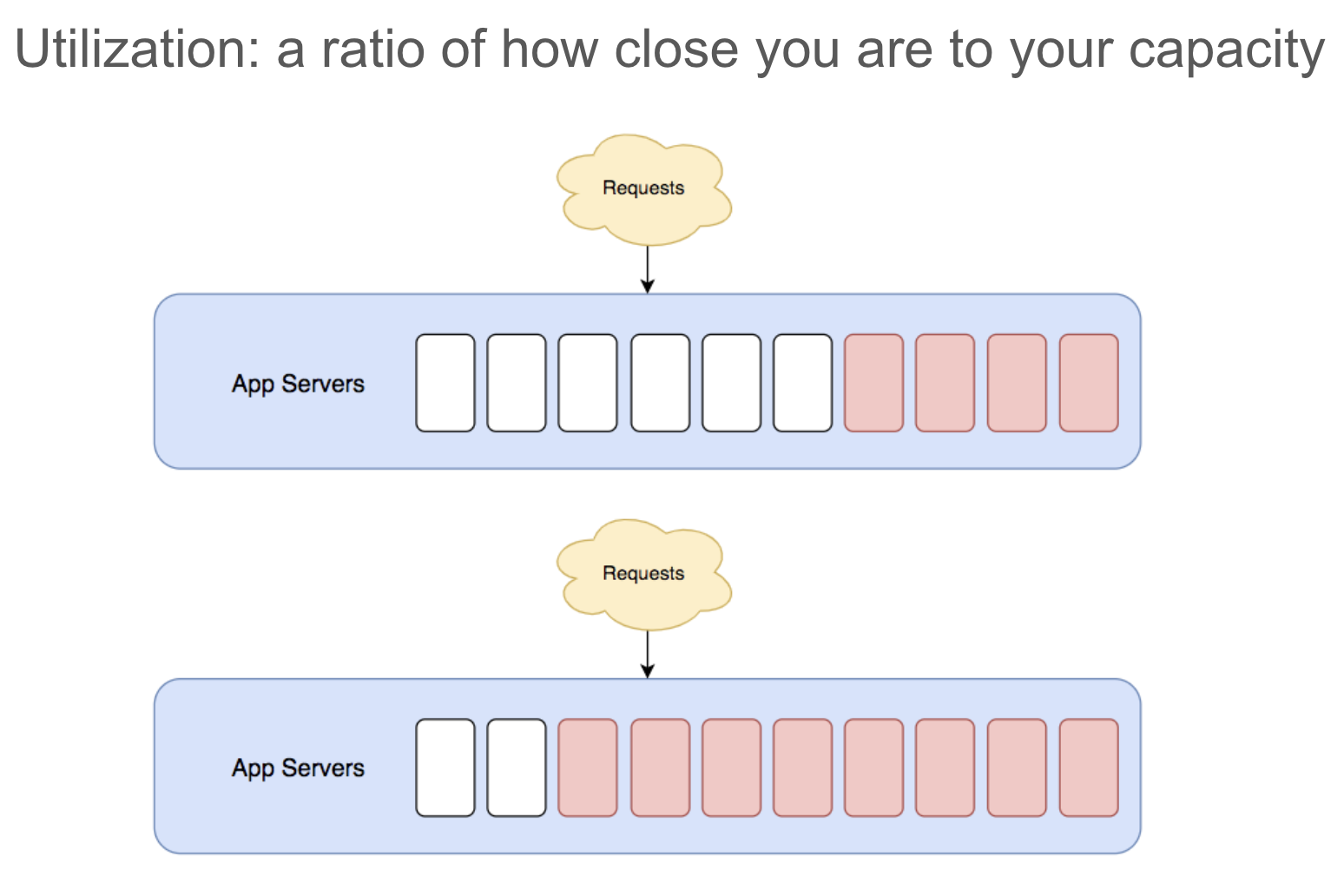
Chapter 3: Load Regulation

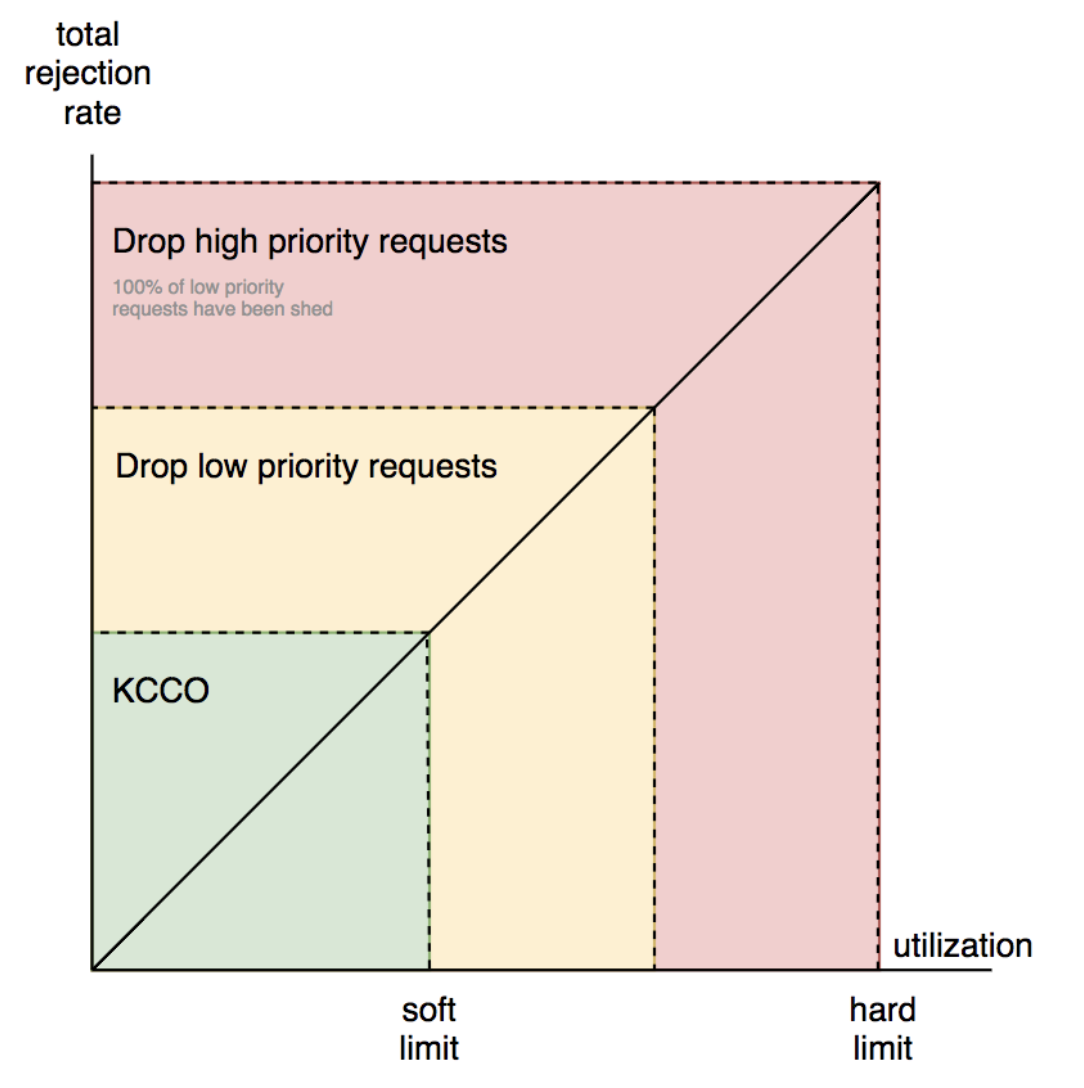
Suppose you now have a reliable signal. What next? I learnt a lot from reading a Google Cloud blog post: Using load shedding to survive a success disaster - CRE life lessons

Appendix: References in the Industry

While I formulate this page, here's a (definitely incomplete) list of references I've collected over the years:

• Site Reliability Engineering: Handling Overload
• Netflix: Performance Under Load
• Using Load Shedding to Survive a Success Disaster
• Netflix Hystrix
• Facebook PSI load shedding
• Great comment on PSI and how it's calculated
• Release notes for PSI
• Linux load average explained (Brendan Gregg)
• How to use BPF to monitor JVM
• runqlen.py
• CPU utilization is "wrong"
• ProxySQL how to reject queries
• Heracles: Improving Resource Efficiency at Scale
• Queues your query waits in
• Introduction to Queueing Theory

to be continued (one day?!)...